বৃত্ত ও বৃত্তের পরিবার

বৃত্ত ও বৃত্তের পরিবার

বৃত্তকাকে বলে?

বৃত্ত: যে বক্র রেখার উপরস্থ সকল বিন্দু সমতলস্থ একটি নির্দিষ্ট বিন্দু হতে সমদূরবর্তী তাকে বৃত্ত বলা হয়। বৃত্ত একটি আবদ্ধ বক্ররেখা, যার অভ্যন্তরে এমন একাটি বিন্দু আছে যা থেকে বৃত্তের উপরের প্রত্যেক বিন্দুর দূরত্ব সমান। এই বিন্দুটিকে বৃত্তের কেন্দ্র বলে।

অথবা, একটি নির্দিষ্ট বিন্দুকে কেন্দ্র করে যদি কোন চলমান বিন্দু সর্বদা সমান দূরত্ব অতিক্রম করে এর চার দিকে এক বার ঘুরে এলে যে বক্র রেখা অংকিত হয় তাকে বৃত্ত বলে।

বৃত্তের ব্যাস কাকে বলে?

বৃত্তের ব্যাস: বৃত্তের পরিধির যে কোন বিন্দু হতে বৃত্তের কেন্দ্রের ভিতর দিয়ে তার বিপরীত বিন্দু পর্যন্ত বিস্তৃত সরল রেখার দূরত্বকে ব্যাস বলে।

ব্যাসকে 2r দ্বারা প্রকাশ করা হয়।

বৃত্তের ব্যাসার্ধ কাকে বলে?

ব্যাসার্ধ: বৃত্তের পরিধির যে কোন বিন্দু হতে বৃত্তের কেন্দ্র পর্যন্ত বিস্তৃত সরল রেখাকে ব্যাসার্ধ বলে। বৃত্তের সকল ব্যাসার্ধের দৈর্ঘ্য একই।

ব্যাসার্ধকে r দ্বারা প্রকাশ করা হয়। 

বৃত্তের জ্যা কাকে বলে?

জ্যা: বৃত্তের পরিধির দুইটি ভিন্ন বিন্দুর সংযোজক রেখাংশকে বৃত্তটির একটি জ্যা বলে।

বৃত্তের পরিধি কাকে বলে?

বৃত্তের পরিধি: বৃত্তের বেড় বা সীমারেখার দৈর্ঘ্যকে বৃত্তের পরিধি বলে। উপরের চিত্রে বৃত্তের পরিধি দেখানো হয়েছে।

বৃত্ত চাপ কাকে বলে?

চাপ: বৃত্তের জ্যা বৃত্তটিকে যে দুটি অংশে বিভক্ত করে তাদেরকে বৃত্তচাপ বলা হয় । চাপ দুইটির একটিকে অপরটির অনুবন্ধী বলে।

অর্ধবৃত্ত কাকে বলে?

অর্ধবৃত্ত: বৃত্তের ব্যাস বৃত্তকে যে দুইটি সমান অংশে বিভক্ত করে তাদের প্রত্যেককে অর্ধবৃত্ত বলে।

অধিচাপ ও উপচাপ কাকে বলে?

অধিচাপ ও উপচাপ: বৃত্তের জ্যা বৃত্তকে যে দুটি অসমান চাপে বিভক্ত করে তার বৃহত্তর চাপটিকে অধিচাপ এবং ক্ষুদ্রতর চাপটিকে উপচাপ বলা হয়।

বৃত্তের একই চাপের উপর দণ্ডায়মান বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক। বিপরীতক্রমে, বৃত্তের একই চাপের উপর দণ্ডায়মান কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ। আবার, অর্ধবৃত্তস্থ কোণ এক সমকোণ বা ৯০°।

ছেদক ও স্পর্কশক কাকে বলে?

ছেদক ও স্পর্শক: সমতলস্থ একটি বৃত্ত ও একটি সরলরেখার যদি দুইটি ছেদবিন্দু থাকে তবে রেখাটিকে বৃত্তের একটি ছেদক বলা হয় এবং যদি একটি ও কেবল একটি ছেদবিন্দু থাকে তবে রেখাটিকে বৃত্তটির একটি স্পর্শক বলা হয়। শেষোক্ত ক্ষেত্রে, সাধারণ বিন্দুটিকে ঐ স্পর্শকের স্পর্শবিন্দু বলা হয়।

বৃত্ত কলা কাকে বলে?

বৃত্তের দুইটি ব্যাসার্ধ ও একটি চাপ দ্বারা গঠিত অঞ্চলকে বৃত্তকলা বা বৃত্তীয় ক্ষেত্র বলে।

বৃত্তের ক্ষেত্রফল নির্ণয়ের সূত্র

বৃত্তের ক্ষেত্রফল নির্ণয়ের সূত্রটি হল πr² 

যেখানে, r হচ্ছে বৃত্তের ব্যাসার্ধ এবং π হচ্ছে একটি ধ্রুবক বা constant যার মান 3.1416 প্রায়। 

একটি বৃত্তের ব্যাস বা ব্যাসার্ধ জানলে আমরা খুব সহজে সেই বৃত্তটির ক্ষেত্রফল নির্ণয় করতে পারব।

ধরুন, একটি বৃত্তের ব্যাস দেওয়া রয়েছে 5 সেন্টিমিটার, এক্ষেত্রে আপনাকে বৃত্তটির ক্ষেত্রফল নির্ণয় করতে হবে। নিম্নে আমরা আপনাকে দেখাচ্ছি কিভাবে আপনি ক্ষেত্রফল নির্ণয় করতে পারবেন।

প্রথমে ব্যাস কে ব্যাসার্ধ পরিণত করতে হবে অর্থাৎ ব্যাসকে দুই দিয়ে ভাগ করলে আমরা ব্যাসার্ধ পাব। অর্থাৎ আমরা পাই বৃত্তটির ব্যাসার্ধ 2.5 সেন্টিমিটার। এখন আমরা হিসাব করলে পাব:

বৃত্তের  ক্ষেত্রফল A=`πr^2`

`\Rightarrow A=\pi(2.5)^2`

`\Rightarrow A=3.1416\times6.25`

`\Rightarrow A=19.63495`

অর্থাৎ বৃত্তের ক্ষেত্রফল 19.63 বর্গসেন্টিমিটার।

এই পদ্ধতিতে আমরা যে কোন বৃত্তের ব্যাস অথবা ব্যাসার্ধ জানার মাধ্যমে খুব সহজে তার ক্ষেত্রফল নির্ণয় করতে পারব। বৃত্তের ক্ষেত্রফল নির্ণয় করা অনেক রকমের গণিতে প্রয়োজন হয়ে থাকে। এমনকি বড় বড় গাণিতিক সমস্যা সমাধানের ক্ষেত্রে এর ব্যবহার হয়ে থাকে।

বৃত্তের পরিধি ও তার অংশ

দ্বিমাত্রিক জ্যামিতিতে বৃত্ত হলো সুষম আবদ্ধ একটি বক্রাকার চিত্র বা বক্ররেখা। তাই বৃত্ত মূলতঃ একটি বদ্ধ বক্ররেখা। একটি বৃত্ত-বক্ররেখার যেকোনো স্থানে কেটে বক্ররেখাটিকে সোজাসুজি টান করলে যে রেখাংশ তৈরি হয়, সেই রেখাংশের দৈর্ঘ্যকে বৃত্তটির পরিধি বলে। আবার বৃত্ত হলো একটি ডিস্কের ধার বা সীমানা। সেই কারণে পরিধি হলো পরিসীমার একটি বিশেষ রূপ। দ্বিমাত্রিক জ্যামিতিতে, পরিসীমা হলো বহুভুজের বাহুগুলোর দৈর্ঘ্যের সমষ্টি।

বৃত্ত, উপবৃত্ত ইত্যাদি কিছু দ্বিমাত্রিক গোলাকার আকার-আকৃতির ক্ষেত্রে, আকৃতিটির চতুর্দিকের মোট দৈর্ঘ্য বা দুরত্বকে পরিধি বলা হলেও বেশিরভাগ দ্বিমাত্রিক আকার-আকৃতির চারদিকের বাহুগুলোর দৈর্ঘ্যের সমষ্টিকে পরিসীমা বলা হয়। যেমন – ত্রিভুজ, চতুর্ভুজ, রম্বস, বর্গক্ষেত্র ইত্যাদি এরা প্রত্যকেই এক একটি বহুভুজ। এসব বহুভুজের বাহুগুলোর দৈর্ঘ্যের সমষ্টি পরিসীমা বলে পরিচিত। পক্ষান্তরে, উপবৃত্তের চতুর্দিকের ধারের দুরত্ব পরিধি বলে অভিহিত।

বৃত্তের পরিধি নির্ণয়ের সূত্র

বৃত্তের পরিধি নির্ণয়ের সূত্রটি হল 2πr যেখানে r হচ্ছে বৃত্তের ব্যাসার্ধ এবং π হচ্ছে একটি ধ্রুবক বা constant যার মান 3.1416 প্রায়। একটি বৃত্তের ব্যাস বা ব্যাসার্ধ জানলে আমরা খুব সহজে সেই বৃত্তটির পরিধি নির্ণয় করতে পারব।

বৃত্তের পরিধি 

`C=2πr`

উদাহরণ:

ধরুন একটি বৃত্তের ব্যাস দেওয়া রয়েছে 10 সেন্টিমিটার, এক্ষেত্রে আপনাকে বৃত্তটির পরিধি নির্ণয় করতে হবে। নিম্নে আমরা আপনাকে দেখাচ্ছি কিভাবে আপনি পরিধি নির্ণয় করতে পারবেন।

প্রথমে ব্যাস কে ব্যাসার্ধ পরিণত করতে হবে অর্থাৎ ব্যাসকে দুই দিয়ে ভাগ করলে আমরা ব্যাসার্ধ পাব। অর্থাৎ আমরা পাই বৃত্তটির ব্যাসার্ধ 5 সেন্টিমিটার। এখন আমরা হিসাব করলে পাব:

বৃত্তের  পরিধি `C=2πr`

`\Rightarrow C=2\times3.1416\times5`

`\Rightarrow C=31.41593`

`⇒C≈31.42`

অর্থাৎ বৃত্তের পরিধি 31.42 সেন্টিমিটার।

এই পদ্ধতিতে আমরা যে কোন বৃত্তের ব্যাস অথবা ব্যাসার্ধ জানার মাধ্যমে খুব সহজে তার পরিধি নির্ণয় করতে পারব। 

বৃত্তের সাধারণ বৈশিষ্ট্যসমূহ

বৃত্তের সংজ্ঞা বিশ্লেষণ করলে বৃত্ত সংক্রান্ত কতকগুলো মৌলিক উপাদান ও বৃত্তের বৈশিষ্ট্য পরিলক্ষিত হয়। আবার বৃত্তের বিভিন্ন অংশ যেমন বৃত্তের কেন্দ্র, বৃত্তের ব্যাসার্ধ, বৃত্তের ব্যাস, বৃত্তের পরিধি, বৃত্তের ক্ষেত্রফল, বৃত্তের স্পর্শক, বৃত্তের প্রতিসমতা ইত্যাদি বিশ্লেষণ করলে বৃত্তের বৈশিষ্ট্য গুলো কি কি তা স্পষ্ট হয়ে ওঠে।

বৃত্ত বিশ্লেষণ করলে যেসব বৃত্তের বৈশিষ্ট্য পরিলক্ষিত হয়, বৃত্ত চিত্র সহ তার একটি তালিকা নিচে উল্লেখ করা হলোঃ

• একটি নির্দিষ্ট দৈর্ঘ্যকে পরিসীমা বিবেচনা করে যেসব দ্বিমাত্রিক ক্ষেত্র যেমন ত্রিভুজ, চতুর্ভুজ, বহুভুজ, বৃত্ত ইত্যাদি অঙ্কন করা যায় তাদের মধ্যে বৃত্ত ক্ষেত্রটির ক্ষেত্রফল হবে সবচেয়ে বেশি।
• বৃত্তের পরিধি ও বৃত্তের ব্যাসার্ধ সমানুপাতিক।
• বৃত্তের একই চাপের উপর দণ্ডায়মান বৃত্তস্থ কোণগুলো পরস্পর সমান।
• বৃত্তের পরিধি ও ব্যাসের অনুপাত সবসময়ই ২২ : ৭, যা π বলে পরিচিত অর্থাৎ, π = ২২৭।
• বৃত্তের দুইটি সমান সমান জ্যা পরস্পরকে ছেদ করলে তাদের একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান।

• একটি বৃত্তের অসংখ্য ব্যাসার্ধ আঁকা যায়।
• একই সমতলে অবস্থিত এবং সমরেখ নয় এমন তিনটি বিন্দু দিয়ে একটি ও কেবল একটি বৃত্ত অঙ্কন করা যায়।
• বৃত্তের সমান সমান জ্যা এর মধ্যবিন্দুগুলো সমবৃত্ত।
• বৃত্তস্থ ট্রাপিজিয়ামের তির্যক বাহুদ্বয় পরস্পর সমান।
• দুইটি সমান্তরাল জ্যা এর মধ্যবিন্দুর সংযোজক সরলরেখা কেন্দ্রগামী এবং জ্যা দুইটির উপর লম্ব।
• বৃত্তের যেকোনো জ্যা এর লম্বদ্বিখণ্ডক কেন্দ্রগামী।
• বৃত্তে অন্তর্লিখিত চতুর্ভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় তা বিপরীত অন্তঃস্থ কোণের সমান।
• বৃত্তস্থ চতুর্ভুজের যেকোনো কোণের সমদ্বিখণ্ডক ও তার বিপরীত কোণের বহির্দ্বিখণ্ডক বৃত্তের উপর ছেদ করে।
• বৃত্তের একই চাপের উপর দণ্ডায়মান কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ।
• সব বৃত্তই পরস্পর সদৃশ।
• যেসব বৃত্তের ব্যাসার্ধ পরস্পর সমান, সেসব বৃত্ত পরস্পর সর্বসম।
• বৃত্তের ক্ষেত্রফল ও তার ব্যাসার্ধের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল সমানুপাতিক।
• বৃত্তের অধিচাপে অন্তর্লিখিত কোণ একটি সূক্ষ্মকোণ।
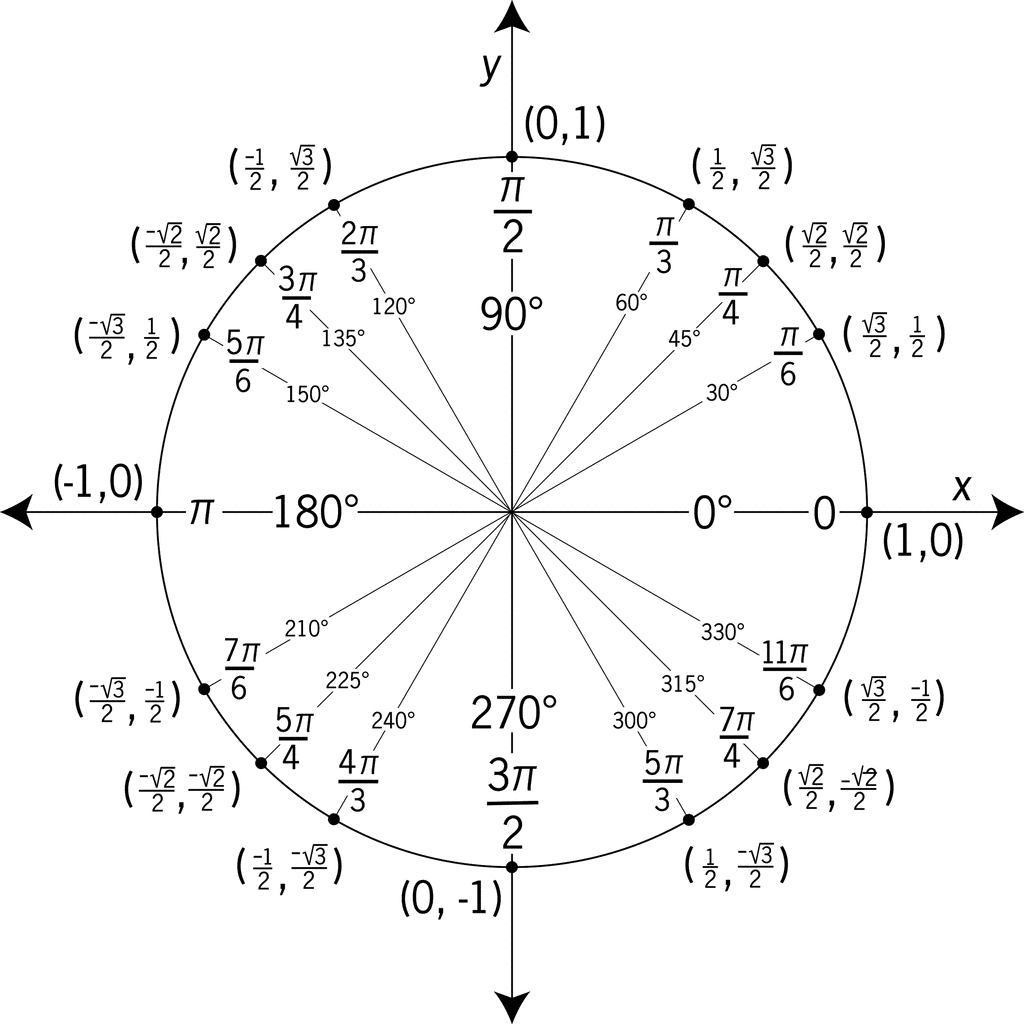
• যে বৃত্তের কেন্দ্র মূলবিন্দু (0,0) এবং ব্যাসার্ধ ১ একক, তার নাম একক বৃত্ত (unit circle)।
• বৃত্তের ব্যাস বৃত্তের ব্যাসার্ধের দ্বিগুণ।
• বৃত্তের প্রত্যেক ছেদকের ছেদবিন্দুদ্বয়ের অন্তর্বর্তী সকল বিন্দু বৃত্তের অভ্যন্তরে থাকে।
• যেকোনো বৃত্তের স্পর্শবিন্দুতে স্পর্শকের উপর অঙ্কিত লম্ব কেন্দ্রগামী।

বৃত্ত সংক্রান্ত যেসব প্রশ্নসমূহ সচরাচর মানুষ করে থাকে।

প্রশ্নঃ ১. বৃত্তের পরিধি নির্ণয়ের সূত্র কি

উত্তরঃ বৃত্তের পরিধি নির্ণয়ের সূত্র কি জানতে হলে, বৃত্তের পরিধি কি তা জানা দরকার। বৃত্তের চতুর্দিকের সীমান্ত বরাবর দৈর্ঘ্যকে বৃত্তের পরিধি বলে। বৃত্তের ব্যাসার্ধ r একক হলে বৃত্তের পরিধি নির্ণয়ের সূত্র হবে 2πr একক যেখানে π একটি গ্রিক অক্ষর এবং π = 3.1416.

∴ বৃত্তের পরিধি = 2πr একক।

প্রশ্ন ২. সমবৃত্ত কাকে বলে ?

উত্তরঃ বৃত্তে অন্তর্লিখিত কোন আবদ্ধ ক্ষেত্রের শীর্ষ বিন্দুসমূহ যদি ঐ বৃত্তের পরিধির উপর অবস্থান করে তবে ঐ বিন্দুসমূহ কে সমবৃত্ত বলে। অন্যভাবে বললে, একই বৃত্তের পরিধির উপর অবস্থিত বিন্দুসমূহকে সমবৃত্ত বলে। যেমনঃ ABCD চতুর্ভুজের শীর্ষবিন্দু চারটি A, B, C ও D একটি বৃত্তের পরিধির উপর অবস্থিত হলে ঐ বিন্দু চারটিকে সমবৃত্ত বলে। তদ্রূপ, P, Q, R, S ও T এই বিন্দু পাঁচটি একই বৃত্তের পরিধির উপর অবস্থিত হলে বিন্দু পাঁচটিকে একত্রে সমবৃত্ত বলা হয়।

প্রশ্ন ৩. বৃত্ত কাকে বলে ?

উত্তর: একটি নির্দিষ্ট বিন্দু থেকে সর্বদা সমান দূরত্ব বজায় রেখে অন্য আরেকটি বিন্দু তার চারদিকে একবার ঘুরে এলে যে গোলাকার ক্ষেত্র তৈরি হয় তাকে বৃত্ত বলে। অন্যভাবে বললে, একটি নির্দিষ্ট বিন্দু থেকে সর্বদা সমান দূরত্ব বজায় রেখে যে আবদ্ধ বক্ররেখা চারদিকে ঘুরে আসে তাকে বৃত্ত বলে।

প্রশ্ন ৪. সমকেন্দ্রিক বৃত্ত কাকে বলে ?

উত্তরঃ একই কেন্দ্র বিশিষ্ট একাধিক বৃত্তকে সমকেন্দ্রিক বৃত্ত বলে। অন্যভাবে বললে, কতকগুলো বৃত্তের কেন্দ্র একই বিন্দু হলে ঐসব বৃত্তসমূহকে সমকেন্দ্রিক বৃত্ত বলে। যেমনঃ মনেকরি, ABC বৃত্তের কেন্দ্র O, PQR বৃত্তের কেন্দ্র O এবং XYZ বৃত্তের O. এখানে তিনটি বৃত্তের কেন্দ্রই O. তাই বৃত্ত তিনটিকে সমকেন্দ্রিক বৃত্ত বলে।

প্রশ্নঃ ৫. একটি বৃত্তের কয়টি অংশ থাকে

উত্তরঃ একটি বৃত্তের কয়টি অংশ থাকে তা এক কথায় জবাব দেওয়া একটু কষ্টকর। তবে সহজ করে বললে, বৃত্তের বিভিন্ন অংশ নিয়ে বৃত্ত গঠিত। একটি সাধারণ বৃত্ত থেকে বৃত্তের বিভিন্ন অংশ চেনা যায় না। বৃত্তের বিভিন্ন অংশ চিহ্নিত করতে চাইলে বৃত্তে তা অংকন করতে হয়। বৃত্তের বিভিন্ন অংশ সমূহ যেমন: বৃত্তের কেন্দ্র, বৃত্তের ব্যাসার্ধ, বৃত্তের ব্যাস, বৃত্তের পরিধি, বৃত্তের ক্ষেত্রফল, বৃত্তের জ্যা, বৃত্তচাপ, অর্ধবৃত্ত চাপ, অর্ধবৃত্ত, বৃত্তাংশ, বৃত্তের ছেদক রেখা, বৃত্তীয় কোণ, অর্ধবৃত্তস্থ কোণ, বৃত্ত কলা ইত্যাদি।

বৃত্ত সম্পর্কিত কিছু সূত্র:

• বৃত্তের ক্ষেত্রের ক্ষেত্রফল =πr² ( যেখানে r বৃত্তের ব্যাসার্ধ)
• গোলকের পৃষ্ঠের ক্ষেত্রফল =4πr²
• গোলকের আয়তন =4÷3(πr³)

বৃত্ত সম্পর্কিত কিছু ধারণা

০১। একই সরলরেখায় অবস্থিত তিনটি বিন্দুর মধ্য দিয়ে কোন বৃত্ত আকা যায়না।
০২। দুটি নির্দিষ্ট বিন্দু দিয়ে ৩টি বৃত্ত আকা যায়।
০৩। একটি বৃত্তের যেকোন দুটি বিন্দুর সংযোজক রেখাকে জ্যা বলা হয়।
০৪। বৃত্তের পরিধি ও ব্যাসের অনুপাতকে π বলে।
০৫। বৃত্তের কেন্দ্র থেকে কোন বিন্দুর দুরত্বকে ওই বৃত্তের ব্যাসার্ধ বলে।
০৬। বৃত্তের সমান সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
০৭। বৃত্তের দুটি জ্যায়ের মধ্যে কেন্দ্রের নিকটতম জ্যাটি অপর জ্যা অপেক্ষা বড়।
০৮।বৃত্তের ব্যাসই বৃত্তের বৃহত্তম জ্যা।
০৯। বৃত্তের যে কোন জ্যা এর লম্বদ্বিখণ্ডক কেন্দ্রগামী।
১০। কোন বৃত্তের ৩টি সমান জ্যা একই বিন্দুতে ছেদ করলে ওই বিন্দুটি বৃত্তের কেন্দ্রে অবস্থিত হবে।
১১। অর্ধবৃত্তস্থ কোন এক সমকোণ।বৃত্ত সম্পর্কিত কিছু ধারণাঃ
১২। একই সরলরেখায় অবস্থিত তিনটি বিন্দুর মধ্য দিয়ে কোন বৃত্ত আকা যায়না।
১৩। দুটি নির্দিষ্ট বিন্দু দিয়ে ৩টি বৃত্ত আকা যায়।
১৪। একটি বৃত্তের যেকোন দুটি বিন্দুর সংযোজক রেখাকে জ্যা বলা হয়।
১৫। বৃত্তের পরিধি ও ব্যাসের অনুপাতকে π বলে।
১৬। বৃত্তের কেন্দ্র থেকে কোন বিন্দুর দুরত্বকে ওই বৃত্তের ব্যাসার্ধ বলে।
১৭। বৃত্তের সমান সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
১৮। বৃত্তের দুটি জ্যায়ের মধ্যে কেন্দ্রের নিকটতম জ্যাটি অপর জ্যা অপেক্ষা বড়।
১৯। বৃত্তের ব্যাসই বৃত্তের বৃহত্তম জ্যা।
২০। বৃত্তের যে কোন জ্যা এর লম্বদ্বিখণ্ডক কেন্দ্রগামী।
২১। কোন বৃত্তের ৩টি সমান জ্যা একই বিন্দুতে ছেদ করলে ওই বিন্দুটি বৃত্তের কেন্দ্রে অবস্থিত হবে।
২২। অর্ধবৃত্তস্থ কোন এক সমকোণ।
২৩। একই সরলরেখায় অবস্থিত তিনটি বিন্দুর মধ্য দিয়ে কোন বৃত্ত আকা যায়না।
২৪। দুটি নির্দিষ্ট বিন্দু দিয়ে ৩টি বৃত্ত আকা যায়।
২৫। একটি বৃত্তের যেকোন দুটি বিন্দুর সংযোজক রেখাকে জ্যা বলা হয়।
২৬। বৃত্তের পরিধি ও ব্যাসের অনুপাতকে π বলে।
২৭। বৃত্তের কেন্দ্র থেকে কোন বিন্দুর দুরত্বকে ওই বৃত্তের ব্যাসার্ধ বলে।
২৮। বৃত্তের সমান সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
২৯। বৃত্তের দুটি জ্যায়ের মধ্যে কেন্দ্রের নিকটতম জ্যাটি অপর জ্যা অপেক্ষা বড়।
৩০। বৃত্তের ব্যাসই বৃত্তের বৃহত্তম জ্যা। 
৩১। বৃত্তের যে কোন জ্যা এর লম্বদ্বিখণ্ডক কেন্দ্রগামী।
৩২। কোন বৃত্তের ৩টি সমান জ্যা একই বিন্দুতে ছেদ করলে ওই বিন্দুটি বৃত্তের কেন্দ্রে অবস্থিত হবে।
৩৩। অর্ধবৃত্তস্থ কোন এক সমকোণ।