সেটের ধারনা - Concepts of Sets

সেটের ধারনা - Concepts of Sets

সেট গণিতের একটি বিশেষ শাখা। জার্মান গণিতবিদ জর্জ ক্যান্টন সর্বপ্রথম সেটের ধারনা দেন। আজ আমরা গণিতের সেট সম্পর্কে বিস্তারিত আলোচনা করবো। এই পোষ্টটি পড়ার পর সেট সম্পর্কে আপনার ধারনা সম্পূর্ণ পরিষ্কার হয়ে যাবে। চলুন তাহলে আমরা সেট সম্পর্কে জানি। 

সেটের বিভিন্ন প্রতীক ও নাম:

১. `\in` = Element (উপাদান)

২. `\not\in` = Not Element (উপাদান নয়)

৩. `\subset` = Sub set (উপসেট)

৪. `\subseteq` = Improper Sub Set (অপ্রকৃত উপসেট)

৫. `\cup` = Union/Cup (সংযোগ)

৬. `\cap` = Intersection/Cap (ছেদ)

৭. `\equiv` = Equivalent Set (সমতুল)

৮. `\phi` = Null Set (ফাঁকা সেট)

৯. U = Universal Set (সার্বিক সেট)

কতিপয় মৌলিক সংজ্ঞা (Some Basic Definitions): 

ক) সেট (Set): জার্মান গণিতবিদ জর্জ ক্যান্টর সর্বপ্রথম সেটের ধারণা দেন। আধুনিক গণিতের হাতিয়ার হিসেবে ইহার ব্যবহার ব্যপক। একই জাতীয় কতগুলো বস্তুর সুনির্ধারিত সংগ্রহকে সেট বলে। একে সাধারণত ইংরেজী বড় অক্ষর A, B, C, D ইত্যাদি দ্বারা প্রকাশ করা হয়। 

যেমন: ছক্কা নিক্ষেপের সম্ভাব্য ফলাফল সমূহের সেট, A={1, 2, 3, 4, 5, 6}

খ) সেটের উপাদান (Elements of a Set): কোন সেটের অন্তর্ভূক্ত প্রত্যেক বস্তুকে  ঐ সেটের উপাদান বলে। একে সাধারণত ইংরেজী ছোট হাতের অক্ষর দ্বারা প্রকাশ করা হয়। যেমন: A={a, b, c, d}

এখানে a হল A সেটের উপাদান। একে গাণিতিক ভাবে `a\in A` লিখা হয়। 

গ) সসীম সেট (Finit Set): যে সেটের উপাদানগুলোর সংখ্যা সুনির্দিষ্ট থাকে, তাকে সসীম সেট বলে। 

যেমন: B={1, 2, 3, 4} । এখানে উপাদান সংখ্যা ৪টি। 

ঘ) অসীম সেট (Infinite Set): যে সেটের উপাদানগুলোর সংখ্যা সুনির্দিষ্ট নয় তাকে অসীম সেট বলে। 

যেমন: B={1, 2, 3, 4, . . . . .} । এখানে উপাদান সংখ্যা কত তা বলা যায় না। 

ঙ) শূণ্য সেট (Null Set): যে সেটে কোন উপাদান থাকে না তাকে শূণ্য সেট বলে। যেমন: বাংলাদেশে ১০ ফুটের অধিক লম্বা লোকের সেট। একে গ্রীক অক্ষল `\phi` দ্বারা প্রকাশ করা হয়। এক্ষেত্রে `\phi` = {}

চ) একক সেট (Unit or Unique Set): যে সেটে একটি মাত্র উপাদান থাকে তাকে একক সেট বলে। যেমন: B={a}

ছ) অভেদ বা সম সেট (Identical or Equal Set): দুটি সেটের উপাদান একই হলে, সেট দুটিকে সমসেট বলে। যেমন: A={2, 5, 9} এবং B={5, 2, 9} হলে, A=B। এক্ষেত্রে A ও B সমসেট।  

 

জ) সমতুল্য সেট (Equivalent Set): যদি কোন সেটের প্রত্যেক উপাদান অপর সেটের প্রত্যেক উপাদানের সাথে এক এক করে মিলানো যায়, তবে উহাদের একটিকে অপরটির সমতুল্য সেট বলে। এক্ষেত্রে `\equiv` প্রতীক ব্যবহার করা হয়। যেমন:

A={a, b, c} এবং B={2, 5, 7}

যদি `a\Rightarrow2,b\Rightarrow5` এবং `c\Rightarrow7` হয় তবে `A\equiv B` হবে। 

ঝ) উপসেট (Sub Set): কোন সেটের সকল উপাদান যদি অন্য কোন সেটে অন্তর্ভূক্ত থাকে তাহলে ঐ সেটকে অন্য সেটের উপসেট বলে। এক্ষেত্রে `\subset` প্রতীক ব্যবহার করা হয়। যেমন: A={2, 3, 5} এবং B={1, 2, 3, 5, 7} । এখানে A হল B সেটের উপসেট। অর্থাৎ `A\subset B`

ঞ) প্রকৃত ও অপ্রকৃত উপসেট (Proper and Improper Sub Set): কোন সেটের উপাদানের চেয়ে উহার উপসেট কমপক্ষে একটি উপাদান কম হলে, ঐ উপসেটকে প্রকৃত উপসেট বলে। ধরি, A একটি সেট এবং B উহার উপসেট। যদি B সেটের প্রতিটি উপাদান সেটে A আছে কিন্তু A সেটের অন্তত একটি উপাদান B সেটের উপাদান না হয়, তাহলে B সেটকে A সেটের প্রকৃত উপসেট বলে। প্রতীকের সাহায্যে `B\subset A` লিখা হয়। যেমন: 

A={1, 5, 7, 8} এবং B={1, 7, 8}

এক্ষেত্রে, B উপসেট A সেটের প্রকৃত উপসেট। অর্থাৎ `B\subset A`

কোন সেটের উপাদান এবং উহার উপসেটের উপাদান একই হলে ঐ উপসেটকে অপ্রকৃত উপসেট বলে। ধরি এবং দুটি সেট। যদি উহাদের উপাদান সমূহ একই রকম হয়, তাহলে উহাদের একটিকে অপরটির অপ্রকৃত উপসেট বলে। প্রতীকের সাহায্যে `B\subseteq A` লিখা হয়। যেমন: 

A={1, 5, 7, 8} এবং B={5, 1, 7, 8}

এক্ষেত্রে, B উপসেট A সেটের অপ্রকৃত উপসেট। অর্থাৎ `B\subseteq A`

ট) সেটের তুলনীয়তা (Comparability of Set): যদি দুটি সেটের মধ্যে একটি অপরটির উপসেট হয় তবে উহাদেরকে তুলনীয় সেট বলে। যেমন: 

A={2, 9, 3} এবং B={3, 9}

যেহেতু B হচ্ছে A সেটের উপসেট।

সুতরাং A ও B সেটদ্বয় তুলনীয় সেট। 

ঠ) নিশ্ছেদ সেট বা বিযুক্ত সেট (Disjoint Set): দুটি সেটের উপাদানগুলোর মধ্যে কোন সাধারণ উপাদান না থাকলে তাহলে উহাদেরকে বিযুক্ত বা নিশ্চেদ সেট বলে। একে সংযোগহীন সেটও বলে। নিম্নে ভেনচিত্রে দেখানো হলো-

ভেনচিত্র: নিশ্চেদ সেট

যেমন: A={2, 3, 5} এবং B={1, 4, 7} 

যেহেতু A এবং B সেটদ্বয়ে কোন সাধারণ উপাদান নেই। অতএব উহারা বিযুক্ত সেট। 

ড) শক্তি সেট (Power Set): কোন সেটের সকল উপসেটের সমন্বয়ে গঠিত সেটকে শক্তি বলে। একে P(S) দ্বারা প্রকাশ করা হয়। যেমন:

A={2, 3}

ইহার উপসেট সমূহ: `\phi,\{2\},\{3\},\{2,3\}`

`\therefore P(S)=\lbrack\phi,\{2\},\{3\},\{2,3\}\rbrack`

ঢ) গুচ্ছ সেট (Family Set): কোন সেটের উপাদানগুলো যদি প্রত্যেকেই একটি সেট হয় তবে ঐ সেটকে পরিবার বা গুচ্ছ সেট বলে। যেমন: 

F=[{1}, {2}] গুচ্ছ সেট। কারণ উহার প্রত্যেক উপাদান একটি সেট নির্দেশ করে। 

ণ) সার্বিক সেট (Universal Set): কোন নির্দিষ্ট বৈশিষ্ট্যের সকল উপাদান নিয়ে যে সেট গঠন করা হয় তাকে সার্বিক সেট বলে। একে U দ্বারা প্রকাশ করা হয়। নিম্নে ভেনচিত্রে তা দেখানো হয়েছে-

ভেনচিত্র: সার্বিক সেট

যেমন: কোন কলেজের সকল শিক্ষকদের আয়ের সেট। 

ধরি, A={2, 3, 5} এবং B={1, 4} হয় তাহলে

সার্বিক সেট, U={1, 2, 3, 4, 5}

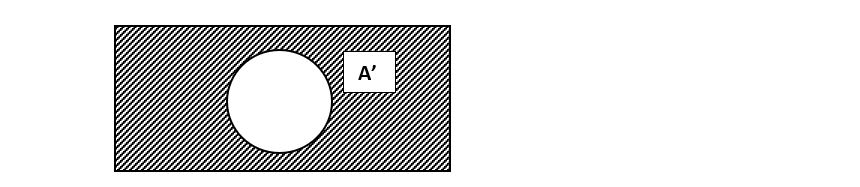
ত) সম্পূর্ক সেট (Complement Set): সার্বিক সেটের উপাদানগুলো হতে কোন সেটের উপাদানগুলো বাদ দিয়ে অবশিষ্ট উপাদানগুলো নিয়ে যে সেট গঠিত হয় তাকে সম্পূর্ক সেট বলে। একে পরিপূরক সেটও বলে। A একটি সেট হলে উহার পরিপূরক সেটকে A' দ্বারা প্রকাশ করা হয়। নিম্নে ভেনচিত্রের সাহায্যে দেখানো হলো-

ভেনচিত্র: সম্পূর্ক সেট

যেমন: 

সার্বিক সেট, U={1, 5, 8, 9, 3} এবং B={1, 8, 9} 

`\therefore B` এর সম্পূরক সেট, B'=U-B 

={1, 5, 8, 9, 3} - {1, 8, 9} 

={5, 3}

 

থ) সুপার সেট (Super Set):  যদি দুটি সেটের মধ্যে কোন সেটের কমপক্ষে একটি উপাদান অপর সেটে না থাকে, তাহলে ঐ সেটকে অপর সেটের সুপার সেট বলে। 

যেমন: 

A={2, 3, 5, 8} এবং B={2, 3, 5}

`\therefore A` সেট B সেটের সুপার সেট। 

ভেন চিত্র (Venn Diagram)

সেট ও সেটের কার্যক্রম যে চিত্রের মাধ্যমে প্রকাশ করা হয় তাকে ভেন চিত্র বলে।  এই চিত্র বিভিন্ন উপসেটের সম্পর্ক নির্দেশ করতে ব্যবহার করা হয়। ব্রিটিশ গণিতবিদ জন ভেন এই চিত্র সর্বপ্রথম ব্যবহার করেন বলে, তাঁর নামনুসারে এই চিত্রের নাম ভেনচিত্র। 

ভেনচিত্রের সাহায্যে সেট উপস্থাপন (Representation of Sets in Venn Diagram): 

ক) ভেনচিত্রে সেটের ইউনিয়ন বা সেটের সংযোগ: 

খ) ভেনচিত্রে সেটের ছেদ:

গ) ভেনচিত্রে বিযুক্ত সেট বা সংযোগহীন সেট: 

ঘ) ভেনচিত্রে সেটের অন্তর: 

ঙ) ভেনচিত্রে পরিপূরক সেট: 

সেটের মৌলিক কায্যক্রম: 

ক) সেটের সংযোগ (Union of Sets): দুই বা ততোধিক সেটের সকল উপাদান নিয়ে যে সেট গঠিত হয় তাকে সংযোগ সেট বলে। উহাদের সংযোগ সেট বলতে এমন একটি নতুন সেট বুঝায় যেখানে A বা B বা উভয়ের উপাদন থাকে। একে `A\cup B` দ্বারা লিখা হয়। নিম্নে ভেনচিত্রের সাহায্যে দেখানো হয়েছে-

যেমন:

A={1, 3, 5} এবং B={1, 2, 3, 4}

সুতরাং, সংযোগ সেট, `A\cup B`={1, 2, 3, 4, 5}

খ) সেটের ছেদ (Intersection of Sets): দুই বা ততোধিক সেটের মধ্যকার সাধারণ উপাদান নিয়ে যে সেট গঠিত হয় তাকে সেটের ছেদ বলে। ধরি, A এবং B দুটি সেট। উহাদের সাধারণ উপাদান নিয়ে গঠিত সেটকে `A\cap B` দ্বারা লিখা হয়। নিম্নে ভেনচিত্রে দেখানো হয়েছে-

যেমন: 

A= {4, 5, 7, 8} এবং B= {3, 5, 8 ,9}

সুতারং, সেটের ছেদ, `A\cap B` = {1, 3}

গ) সেটের অন্তর (Difference of Sets): কোন সেটের যে উপাদানগুলো অপর সেটে নেই, উহাদের সেটকে সেটের অন্তর বলে। ধরি, A এবং B দুটি সেট। A সেট হতে B সেটের উপাদান সমূহ বাদ দিয়ে গঠিত অন্তর সেটকে A-B দ্বারা লেখা হয়। নিম্নে ভেনচিত্রে দেখানো হয়েছে-

যেমন:

A={4, 5, 7, 8} এবং B={3, 5, 8, 9}

সুতারং অন্তর সেট, A-B={4, 7}