কোণ: কোণ নিয়ে বিস্তারিত আলোচনা

কোণ কাকে বলে?

কোণ এর ইংরেজি Angle (বাংলা পরিভাষা কোণ) শব্দটি লাতিন শব্দ angulus থেকে এসেছে যার অর্থ ধার।

দুইটি রশ্মির প্রান্তবিন্দু পরস্পর মিলিত হলে মিলিত বিন্দুতে কোণ উৎপন্ন হয়। অন্যভাবে বললে, দুইটি রশ্মির প্রান্তবিন্দু পরস্পর মিলিত হয়ে যে আকৃতি ধারণ করে তাকে কোণ বলে।

আবার, দুইটি রেখাংশ পরস্পর প্রান্তবিন্দুতে মিলিত হয়ে যে জ্যামিতিক আকার ধারণ করে তাকে কোণ বলে। 

তাহলে সহজ করে বললে, দুইটি সরলরেখা পরস্পর মিলিত হলে কোণ উৎপন্ন হয়। এরূপ দুইটি সরলরেখা পরস্পর ছেদ করলে ছেদ বিন্দুতে চারটি কোণ উৎপন্ন হয়।

যদি দুইটি সরলরেখা পরস্পরের সাথে কোনো বিন্দুতে মিলিত হয়, তবে মিলন বিন্দুতে কোণ উৎপন্ন হয়। আবার, দুটি সরলরেখা তির্যকভাবে পরস্পরের সাথে মিলিত হলে মিলিত বিন্দুতে কোণ উৎপন্ন হয়। সরল রেখা দুইটিকে কোণের বাহু বলা হয়। সরলরেখা দুটির সাধারণ প্রান্তবিন্দুটিকে কোণের শীর্ষ বলে।

 

চিত্র: সকল প্রকার কোণ

তাহলে প্রাথমিকভাবে লক্ষ্য করা যাচ্ছে যে,

• দুইটি রশ্মি পরস্পর ছেদ করলে কোণ উৎপন্ন হয়।
• দুইটি পরস্পরচ্ছেদী সমতল দ্বারা কোণ উৎপন্ন হয়।
• দুইটি বক্ররেখা পরস্পর ছেদ করলে ছেদ বিন্দুতে কোণ উৎপন্ন হয়।

 

কোণের অভ্যন্তর

কোণের বাহুদ্বয়ের উপর অবস্থিত সকল বিন্দু ব্যতীত কোণের অভ্যন্তরস্থ সকল বিন্দুর সেটকে কোণের অভ্যন্তর বলে।

চিত্র: কোণের অভ্যন্তর ও কোণের বহির্ভাগ

চিত্রে, OC ও OD রেখাংশ পরস্পর O বিন্দুতে মিলিত হয়েছে। ফলে, O বিন্দুতে ∠COD উৎপন্ন হয়েছে। OC ও OD বাহুদ্বয়ের উপর অবস্থিত সকল বিন্দু ব্যতীত OD এর যে দিকে C আছে অর্থাৎ OD এর উপরের দিকের সকল বিন্দু এবং OC এর যে দিকে D আছে অর্থাৎ OC এর নিচের দিকের সকল বিন্দুর সেট হলো কোণের অভ্যন্তর। চিত্রে, ∠COD এর অভ্যন্তরে সকল অসংখ্য কালো বিন্দুর সেট হলো কোণের অভ্যন্তর। 

কোণের বহির্ভাগ

কোণের বাহুদ্বয়ের উপর অবস্থিত নয় এবং কোণের অভ্যন্তরস্থ কোন বিন্দু নয় সমতলে অবস্থিত এমন সকল বিন্দুর সেটকে কোণের বহির্ভাগ বলে।

 

কোণ কত প্রকার

কোণের নির্দিষ্ট প্রকারভেদ করা একটু কঠিন। তবে আকার-আকৃতি, গঠন ও পরিমাপের ভিত্তিতে কোণের একটি তালিকা নিচে দেওয়া হলোঃ

• শুণ্য কোণ
• সূক্ষ্মকোণ
• সমকোণ
• স্থূলকোণ
• সরলকোণ
• প্রবৃদ্ধ কোণ
• পূর্ণ কোণ
• তির্যক কোণ
• বিপ্রতীপ কোণ
• সন্নিহিত কোণ
• পূরক কোণ
• সম্পূরক কোণ
• পরিপূরক কোণ
• অনুরূপ কোণ
• একান্তর কোণ
• ধারাবাহিক অন্তঃস্থ কোণ 

শুণ্য কোণ

যে কোণের পরিমাপ 0° তাকে শুণ্য কোণ বলে। এক্ষেত্রে, আসলে কোনো কোণ উৎপন্ন হয়নি।

 

চিত্র: একটি শুণ্য কোণ

চিত্রে, OB রশ্মি প্রান্তবিন্দু O কে স্থির রেখে ঘড়ির কাটার বিপরীত দিকে ঘুড়ে OB অবস্থানে ∠BOB=0° কোণ উৎপন্ন করেছে। এখানে OB রশ্মি আদি অবস্থান থেকে কোনো দিকে না ঘুড়ে আদি অবস্থান OB -তেই আছে। ফলে কোনো কোণ উৎপন্ন হয়নি বা উৎপন্ন কোণের পরিমাপ 0°। অন্যভাবে বললে, OB রশ্মি প্রান্তবিন্দু O কে স্থির রেখে ঘড়ির কাটার বিপরীত দিকে ঘুড়ে OA অবস্থানে ∠AOB=0° কোণ উৎপন্ন করেছে। এখানে OA ও OB একই সরলরেখা বরাবর অবস্থান করছে। তাই উৎপন্ন কোণের পরিমান 0°।

সূক্ষ্মকোণ কোণ

এক সমকোণ বা ৯০° অপেক্ষা ছোট কোণকে সূক্ষ্মকোণ বলে।

চিত্র: একটি সূক্ষ্মকোণ 

চিত্রে, OB রশ্মির সাথে ∠AOB এবং ∠COB দুইটি কোণ উৎপন্ন হয়েছে। এখানে CO⊥OB, অর্থাৎ ∠COB=৯০° এবং ∠AOB < ∠COB. সুতরাং, ∠AOB একটি সূক্ষ্মকোণ। 

সমকোণ

যে কোণের পরিমাপ ৯০° তাকে সমকোণ বলে।

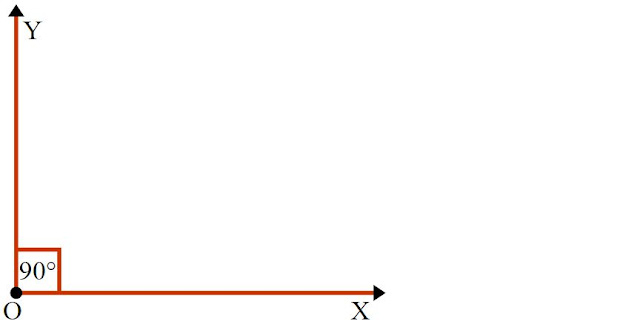চিত্র: একটি সমকোণ

চিত্রে, OX রশ্মি আদি অবস্থান থেকে O বিন্দুতে ঘড়ির কাঁটার ঘূর্ণয়নের বিপরীত দিকে ঘুড়ে আবার OY অবস্থানে ∠XOY উৎপন্ন করেছে। এখানে ∠XOY= ৯০°। 

সুতরাং, এটি একটি সমকোণ। 

স্থূলকোণ

৯০° অপেক্ষা বড় এবং ১৮০° অপেক্ষা ছোট কোণকে স্থূলকোণ বলে। অন্যভাবে বলা যায়, সমকোণ অপেক্ষা বড় এবং সরলকোণ অপেক্ষা ছোট কোণকে স্থূলকোণ বলে।

 

চিত্র: একটি স্থূলকোণ

চিত্রে, AB রশ্মির O বিন্দুতে ∠BOC, ∠BOD এবং ∠AOB তিনটি কোণ উৎপন্ন হয়েছে। এখানে CO⊥AB, অর্থাৎ ∠BOC=৯০°. আবার, ∠AOB একটি সরলকোণ অর্থাৎ, ∠AOB=১৮০°. তাহলে, ∠BOC < ∠BOD < ∠AOB. অর্থাৎ, ৯০°< ∠BOD < ১৮০°।

সুতরাং, ∠BOD একটি স্থূলকোণ।

 

সরলকোণ

যে কোণের পরিমাপ ১৮০° তাকে সরলকোণ বলে।

চিত্র: একটি সরলকোণ চিত্র

চিত্রে, AB একটি সরলরেখা এবং O, AB এর উপর একটি বিন্দু। O বিন্দুতে OC⊥AB. ফলে ∠AOC=∠BOC=90°. O বিন্দুতে আরেকটি ∠AOB উৎপন্ন হয়েছে। 

তাহলে, ∠AOB = ∠AOC + ∠BOC

বা, ∠AOB = ৯০° + ৯০°

∴ ∠AOB = ১৮০°

সুতরাং, ∠AOB একটি সরলকোণ।

প্রবৃদ্ধ কোণ

১৮০° অপেক্ষা বড় এবং ৩৬০° অপেক্ষা ছোট কোণকে প্রবৃদ্ধ কোণ বলে। অন্যভাবে বলা যায়, সরলকোণ অপেক্ষা বড় এবং পূর্ণ কোণ বা ৩৬০° অপেক্ষা ছোট কোণকে প্রবৃদ্ধ কোণ বলে।

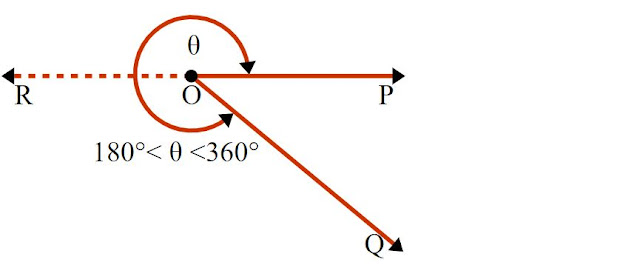চিত্র: একটি প্রবৃদ্ধ

চিত্রে, OP রশ্মি আদি অবস্থান থেকে O বিন্দুতে ঘড়ির কাঁটার ঘূর্ণয়নের বিপরীত দিকে ঘুড়ে OQ অবস্থানে ∠POQ উৎপন্ন করেছে। আবার সরলকোণ ∠POR = ১৮০°। তাহলে, ∠POQ কোণটি ১৮০° অপেক্ষা বড় এবং ৩৬০° অপেক্ষা ছোট।

অর্থাৎ, ১৮০° < ∠POQ < ৩৬০°.

সুতরাং, ∠POQ একটি প্রবৃদ্ধ কোণ।

পূর্ণকোণ

যে কোণের পরিমাপ ৩৬০° তাকে পূর্ণকোণ বলে। অন্যভাবে বলা যায়, একটি রশ্মি তার আদি অবস্থান থেকে ঘুরে আবার একই অবস্থান ফিরে আসলে যে কোণ উৎপন্ন হয় তাকে পূর্ণকোণ বলে। এ রকম একটি রশ্মি একবার ঘুরে আসলে রশ্মির প্রান্তবিন্দুতে উৎপন্ন কোণের পরিমাপ হয় ৩৬০°। তাই পূর্ণকোণের মান ৩৬০°।

চিত্র: একটি পূর্ণকোণ

চিত্রে, OQ রশ্মি আদি অবস্থান থেকে O বিন্দুতে ঘড়ির কাঁটার ঘূর্ণয়নের বিপরীত দিকে ঘুড়ে আবার OQ অবস্থানে ফিরে আসলে উৎপন্ন কোণের পরিমান হয় θ = ৩৬০°।

অর্থাৎ, উৎপন্ন কোণের পরিমান θ হলে,

θ = ∠QOS + ∠SOP + ∠POT + ∠TOQ

বা, θ = ৯০° + ৯০° + ৯০° + ৯০°

∴ θ = ৩৬০°

সুতরাং, θ একটি পূর্ণকোণ।

তির্যক কোণ

যে কোণের পরিমাপ ৯০° নয় বা ৯০° এর কোনো গুণিতক নয় তাকে তির্যক কোণ বলে। অন্যভাবে বলা যায়, যে কোণের মান সমকোণের কোন গুণিতক নয় তাকে তির্যক কোণ বলে। সেই হিসাবে, সব সূক্ষ্মকোণ এবং স্থূলকোণই এক একটি তির্যক কোণ বলে পরিচিত।

চিত্র: কতকগুলো তির্যক।

চিত্রে, OB রশ্মির সাথে O বিন্দুতে ধনাত্মক দিকে অর্থাৎ, ঘড়ির কাঁটার ঘূর্ণয়নের বিপরীত ∠BOE একটি সূক্ষ্মকোণ, ∠BOF একটি স্থূলকোণ এবং ∠BOG ও ∠BOH আরও দুইটি প্রবৃদ্ধ কোণ উৎপন্ন করেছে। কোণগুলোর কোনটিই সমকোণ বা ৯০° নয় এবং কোনটিই সমকোণের গুণিতকও নয়। তাই এরা সবাই এক একটি তির্যক কোণ। আবার,

 ∠BOC = ৯০°,

∠BOA = ১৮০°

∴ ∠BOA = ২ × ৯০°,

∠BOD = ২৭০°

∴ ∠BOD = ৩ × ৯০°,

∠BOB = ৩৬০° [∵ একটি পরিপূর্ণ ঘূর্ণন = পূর্ণ কোণ]

∴ ∠BOB = ৪ × ৯০°

দেখা যাচ্ছে যে, ∠BOC, ∠BOA, ∠BOD এবং ∠BOB এরা সবাই সমকোণের এক একটি গুণিতক । সুতরাং, এদের কোনটিই তির্যক কোণ নয়। অতএব, সমকোণ, সরলকোণ এবং পূর্ণকোণ কেউই তির্যক কোণ নয়।

বিপ্রতীপ কোণ

একটি কোণের বিপরীত রশ্মি দুইটি ঐ কোণের বিপরীতে যে কোণ উৎপন্ন করে তাকে পূর্বের কোণের বিপ্রতীপ কোণ বলে। অন্যভাবে বলা যায়, দুইটি পরস্পরচ্ছেদী সরলরেখা কোনো একটি বিন্দুতে মিলিত হলে, মিলিত বিন্দুতে দুই জোড়া বিপরীত কোণ উৎপন্ন হয়, প্রতিজোড়া বিপরীত কোণের একটিকে অপরটির বিপ্রতীপ কোণ বলে। বিপ্রতীপ কোণদ্বয় পরস্পর সমান হয়।

চিত্র: বিপ্রতীপ কোণ।

চিত্রে, AB ও CD সরলরেখা দুইটি পরস্পর O বিন্দুতে ছেদ করেছে। ফলে O বিন্দুতে ∠AOD, ∠AOC, ∠COB, এবং ∠BOD চারটি কোণ উৎপন্ন হয়েছে। আবার, ∠AOD কোণের বাহু দুইটির বিপরীত রশ্মি দ্বারা ∠COB উৎপন্ন হয়েছে। সুতরাং, ∠AOD এর বিপ্রতীপ ∠COB.

তদ্রূপ, ∠AOC কোণের বাহু দুইটির বিপরীত রশ্মি দ্বারা ∠BOD উৎপন্ন হয়েছে। সুতরাং, ∠AOC এর বিপ্রতীপ ∠BOD.

আবার, বিপ্রতীপ কোণগুলো পরস্পর সমান।

সুতরাং, ∠AOD = ∠COB এবং ∠AOC = ∠BOD.

সন্নিহিত কোণ

একই সমতলে অবস্থিত দুইটি কোণের শীর্ষবিন্দু ও একটি রশ্মি যদি সাধারণ হয় এবং কোণ দুইটি, সাধারণ রশ্মির বিপরীত দিকে অবস্থান করে, তবে কোণ দুইটিকে পরস্পর সন্নিহিত কোণ বলে। যদি একই শীর্ষবিশিষ্ট দুইটি কোণের একটি সাধারণ বাহু থাকে এবং কোণ দুইটির কোনো অভ্যন্তরস্থ বিন্দু সাধারণ না হয়, তাহলে কোণ দুইটিকে পরস্পর সন্নিহিত কোণ বলে।

চিত্র: সন্নিহিত কোণ।

চিত্রে, OA এবং OB রশ্মিদ্বয় O বিন্দুতে ∠AOB উৎপন্ন করেছে। আবার, OA এবং OC রশ্মিদ্বয় O বিন্দুতে ∠AOC উৎপন্ন করেছে। উভয় কোণের শীর্ষবিন্দু O সাধারণ এবং উভয় কোণের সাধারণ বাহু OA. আবার কোণ দুইটি, সাধারণ বাহু OA বিপরীত দিকে অবস্থিত। তাছাড়া কোণ দুইটির অভ্যন্তরস্থ কোনো বিন্দু সাধারণ নয়। অতএব, কোণ দুইটি পরস্পর সন্নিহিত কোণ।

সুতরাং, ∠AOB এবং ∠AOC কোণ দুইটি সন্নিহিত কোণ। 

পূরককোণ

দুইটি কোণের যোগফল ৯০° বা এক সমকোণ হলে কোণ দুইটির একটিকে অপরটির পূরক কোণ বলে। পরস্পর পূরক কোণ দুইটি যদি সন্নিহিত কোণ হয়, তবে সন্নিহিত কোণ দুইটির সাধারণ বাহু ব্যতীত অপর বাহু দুইটি বাহু পরস্পর লম্ব হয়। ইউক্লিডিও জ্যামিতি অনুযায়ী, একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের একটি অপরটির পূরক কোণ।

কারণ মনেকরি, সমকোণী ত্রিভুজ ABC -এ ∠B = ৯০°। আবার ত্রিভুজের তিনকোণের সমষ্টি ১৮০°.

 ∴ ∠A + ∠B + ∠C = ১৮০°

বা, ∠A + ৯০° + ∠C = ১৮০°

বা, ∠A + ∠C = ১৮০° - ৯০°

∴ ∠A + ∠C = ৯০°

অতএব, ∠A এবং ∠C পরস্পর পূরক কোণ। 

চিত্র: পূরক কোণ।

চিত্রে, OM রশ্মির O বিন্দুতে ∠MOL এবং ∠LON দুইটি কোণ উৎপন্ন হয়েছে। এখন, ∠MOL + ∠LON = এক সমকোণ বা ৯০°।

সুতরাং, ∠MOL এবং ∠LON কোণ দুইটি পরস্পর পূরক।

তাছাড়া, পূরক কোণ দুইটি পরস্পর সন্নিহিত কোণ।

বি:দ্র: কোনো একটি কোণ এবং সমকোণ বা ৯০° থেকে ঐ কোণের বিয়োগফল করে প্রাপ্ত কোণ পরস্পর পূরক। অর্থাৎ, কোণ A এবং (90°-A) কোণ দুইটি পরস্পর পূরক।

সম্পূরককোণ

দুইটি কোণের যোগফল ১৮০° বা দুই সমকোণ হলে কোণ দুইটির একটিকে অপরটির সম্পূরক কোণ বলে।

অতএব পরস্পর সম্পূরক কোণ দুইটির সমষ্টি একটি সরলকোণ তৈরি করে। পরস্পর সম্পূরক কোণ দুইটি যদি সন্নিহিত কোণ হয়, তবে সন্নিহিত কোণ দুইটির সাধারণ বাহু ব্যতীত অপর বাহু দুইটি একই সরলরেখায় অবস্থিত হয়। এই ক্ষেত্রে, কোণ দুইটি রৈখিক যুগল কোণ বলেও পরিচিত। সম্পূরক কোণ দুইটি একই রেখায় হতে হবে - এমন কোনো শর্ত নেই। সম্পূরক কোণ দুইটি আলাদা দুই জায়গাতেও থাকতে পারে। যেমন - সামান্তরিকের সন্নিহিত কোণ দুইটি পরস্পর সম্পূরক। আরও একটু সুস্পষ্ট করে বললে, ABCD একটি সামান্তরিক হলে, এর যেকোনো বাহু সংলগ্ন কোণ দুইটির যোগফল ১৮০°. আবার বৃত্তে অন্তর্লিখিত চতুর্ভুজের যে কোনো দুইটি বিপরীত কোণ পরস্পর সম্পূরক। অর্থাৎ, বৃত্তে অন্তর্লিখিত চতুর্ভুজের যে কোনো দুইটি বিপরীত কোণের সমষ্টি দুই সমকোণ বা ১৮০°।

 

চিত্র: পরস্পর সম্পূরক কোণ।

চিত্রে, XY রেখার O বিন্দুতে ∠YOZ এবং ∠ZOX দুইটি কোণ উৎপন্ন হয়েছে। এখন, ∠YOZ + ∠ZOX = সরলকোণ বা ১৮০°।

সুতরাং, ∠YOZ এবং ∠ZOX কোণ দুইটি পরস্পর সম্পূরক।

তাছাড়া, কোণ দুইটি পরস্পর সন্নিহিত কোণ।

পরিপূরক কোণ

দুইটি কোণের যোগফল ৩৬০° বা চার সমকোণ হলে কোণ দুইটিকে পরস্পর পরিপূরক কোণ বলে।

 কোনো একটি কোণ এবং চার সমকোণ বা ৩৬০° থেকে ঐ কোণের বিয়োগফল করে প্রাপ্ত কোণ দুইটি পরস্পর পরিপূরক। অর্থাৎ, কোণ A এবং (৩৬০° - A) কোণ দুইটি পরস্পর পরিপূরক।

চিত্র: পরস্পর পরিপূরক কোণ।

অনুরূপ কোণ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়া কোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যেসব কোণ জোড়া ছেদকের একই পাশে অবস্থান করে এবং কোণ দুইটির একটি অন্তঃস্থ কোণ এবং অপরটি বহিঃস্থ কোণ হয়, সেই কোণ জোড়াকে পরস্পর অনুরূপ কোণ বলে। অনুরূপ কোণকে আরেকভাবে সংজ্ঞায়িত করা যায় - তা হলোঃ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে যে চার জোড়া বা আটটি কোণ উৎপন্ন হয়, তাদের মধ্যে প্রত্যেক জোড়ার অন্তর্গত কোণ দুইটিকে পরস্পর অনুরূপ কোণ বলা হয় যদি ও কেবল যদি তারা নিচের শর্তগুলো পূরণ করেঃ

 অনুরূপ কোণ হওয়ার শর্ত

• কোণ দুইটির শীর্ষবিন্দু ভিন্ন হয়।
• কোণ দুইটির উভয়েই ছেদকের একই পাশে অবস্থান করে।
• কোণ দুইটির একটি অন্তঃস্থ কোণ এবং অপরটি বহিঃস্থ কোণ হয়।
• এরূপ চার জোড়া কোণ পাওয়া যায়।

চিত্র: চার জোড়া অনুরূপ কোণ।

একান্তর কোণ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়া কোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যেসব কোণ জোড়া ছেদকের বিপরীত পাশে অবস্থান করে এবং কোণ দুইটির উভয়েই অন্তঃস্থ কোণ অথবা উভয়েই বহিঃস্থ কোণ হয়, সেই কোণ জোড়াকে পরস্পর একান্তর কোণ বলে। একান্তর কোণকে অন্যভাবে সংজ্ঞায়িত করলে দাঁড়ায়ঃ

 

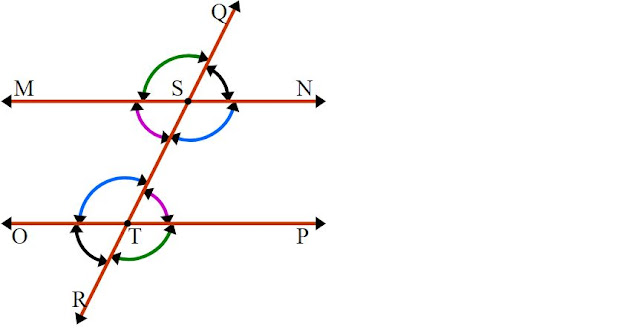চিত্র: চার জোড়া একান্তর কোণ।

দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে যে চার জোড়া বা আটটি কোণ উৎপন্ন হয়, তাদের মধ্যে প্রত্যেক জোড়ার অন্তর্গত কোণ দুইটিকে পরস্পর একান্তর কোণ বলা হয় যদি ও কেবল যদি তারা নিচের শর্তগুলো পূরণ করেঃ

একান্তরকোণ হওয়ার শর্ত

• কোণ দুইটির শীর্ষবিন্দু ভিন্ন হয়।
• কোণ দুইটি ছেদকের বিপরীত পাশে অবস্থান করে।
• কোণ দুইটির উভয়েই অন্তঃস্থ কোণ অথবা উভয়েই বহিঃস্থ কোণ হয়।
• এরূপ চার জোড়া কোণ পাওয়া যায়।

ধারাবাহিক অন্তঃস্থ কোণ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়া কোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যে দুই জোড়া কোণ ছেদকের একই পাশে অবস্থান করে এবং কোণ দুইটির উভয়েই অন্তঃস্থ কোণ হয়, সেই কোণ জোড়াকে পরস্পর ধারাবাহিক অন্তঃস্থ কোণ বলে। ধারাবাহিক অন্তঃস্থ কোণকে অন্যভাবে সংজ্ঞায়িত করলে দাঁড়ায়ঃ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে যে চার জোড়া বা আটটি কোণ উৎপন্ন হয়, তাদের মধ্যে যে দুই জোড়ার প্রত্যেক জোড়ার অন্তর্গত কোণ দুইটিকে পরস্পর ধারাবাহিক অন্তঃস্থ কোণ বলা হয় যদি ও কেবল যদি তারা নিচের শর্তগুলো পূরণ করেঃ

ধারাবাহিক আন্তঃস্থ কোণ হওয়ার শর্ত 

• কোণ দুইটির শীর্ষবিন্দু ভিন্ন হয়।
• কোণ দুইটি ছেদকের একই পাশে অবস্থান করে।
• কোণ দুইটির উভয়েই অন্তঃস্থ কোণ হয়।
• এরূপ দুই জোড়া কোণ পাওয়া যায়।

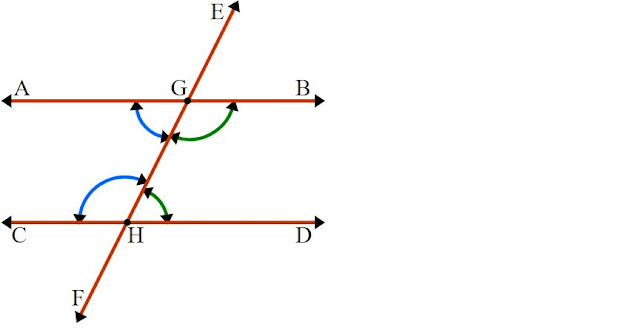চিত্র: দুই জোড়া ধারাবাহিক অন্তঃস্থ কোণ।

কোণ বিষয়ে যে প্রশ্নগুলো করা হয়ে থাকে-

প্রশ্ন ১. বহিঃস্থ কোণ কাকে বলে?

উত্তরঃ বহুভুজের একটি বাহুকে বর্ধিত করলে বর্ধিত রেখাংশ অপর বাহুর সাথে যে কোণ উৎপন্ন করে তাকে বহিঃস্থ কোণ বলে। যেকোনো বহুভুজের অন্তঃস্থ কোণ ও বহিঃস্থ কোণের সমষ্টি দুই সমকোণ বা ১৮০°। একারণে কোনো বহুভুজের অন্তঃস্থ কোণ ও বহিঃস্থ কোণ পরস্পর সম্পূরক কোণ।

প্রশ্ন ২. অন্তঃস্থ কোণ কাকে বলে?

উত্তরঃ বহুভুজের অভ্যন্তরে দুটি বাহুর ছেদ বিন্দুতে যে কোণ উৎপন্ন হয় তাকে অন্তঃস্থ কোণ বলে। যেকোনো বহুভুজের দুইটি বাহু পরস্পর যে বিন্দুতে মিলিত হয় তাকে শীর্ষবিন্দু বলে। আর শীর্ষবিন্দুতে যে কোণ উৎপন্ন হয় তাকে অন্তঃস্থ কোণ বলে। বহুভুজের প্রত্যেকটি শীর্ষবিন্দুতে একটি ও কেবল একটি অন্তঃস্থ কোণ উৎপন্ন হয়। যেমন: ত্রিভুজের তিনটি অন্তঃস্থ কোণ ও চতুর্ভুজের চারটি অন্তঃস্থ কোণ উৎপন্ন হয়।

প্রশ্নঃ ৩. কোণ কত প্রকার?

উত্তরঃ কোণ কত প্রকার -এ প্রশ্নটির উত্তর এক কথায় দেওয়া যায় না। কোণের বিভিন্ন ধরণ রয়েছে। কোনো কোণ এককভাবে গঠিত হয়; আবার কোনো কোনো কোণ জোড়ায় জোড়ায় গঠিত হয়।

এককভাবে গঠিত কোণগুলো হলো: শুণ্য কোণ, সূক্ষ্মকোণ, সমকোণ, স্থূলকোণ, সরলকোণ, প্রবৃদ্ধ কোণ, পূর্ণ কোণ ও তির্যক কোণ।

আবার, জোড়ায় জোড়ায় গঠিত কোণগুলো হলো: বিপ্রতীপ কোণ, সন্নিহিত কোণ, পূরক কোণ, সম্পূরক কোণ, পরিপূরক কোণ, অনুরূপ কোণ ও ধারাবাহিক অন্তঃস্থ কোণ বা ছেদকের পাশে উৎপন্ন অন্তঃস্থ কোণ।

প্রশ্নঃ ৪. বহুভুজের অন্তঃকোণ নির্ণয়ের সূত্র?

উত্তরঃ কোনো সুষম বহুভুজের বাহুর সংখ্যা n এবং প্রতিটি অন্তঃকোণের পরিমাপ θ হলে বহুভুজের অন্তঃকোণ নির্ণয়ের সূত্র, 

`\theta=\frac{\left(n-2\right)}n\times180^\circ`

∴ সুষম বহুভুজের অন্তঃকোণ নির্ণয়ের সূত্র, 

`\theta=\frac{\left(n-2\right)}n\times180^\circ`

প্রশ্নঃ ৫. একটি কোণের কয়টি শীর্ষবিন্দু থাকে

উত্তরঃ একটি কোণের শীর্ষবিন্দুতে কোণ উৎপন্ন হয়। অতএব, একটি কোণের একটি ও কেবল একটি শীর্ষবিন্দু থাকে।

প্রশ্নঃ ৬. কেন্দ্রস্থ কোণ কাকে বলে

উত্তরঃ কোন বৃত্তচাপের প্রান্তদ্বয় হতে সৃষ্ট দুটি রেখাংশ বৃত্তের কেন্দ্রে মিলিত হয়ে যে কোণ উৎপন্ন করে তাকে কেন্দ্রস্থ কোণ বলে। অন্যভাবে বললে, কোনো বৃত্তচাপ দ্বারা কেন্দ্রে উৎপন্ন কোণকে কেন্দ্রস্থ কোণ বলে। তাই, যেকোনো বৃত্তচাপ বৃত্তের কেন্দ্রে একটি ও কেবল একটি কেন্দ্রস্থ কোণ উৎপন্ন করে।

👉বিভিন্ন পরীক্ষার প্রস্তুতির জন্য বাংলা সাহিত্য পড়ুন এখানে।